Curriculum on Self-Organizing Networked Systems
Contents
- 1 Curriculum
- 1.1 Core Courses
- 1.1.1 Introduction to Self-Organizing Networked Systems
- 1.1.2 Dynamical Systems
- 1.1.3 Network Theory
- 1.1.4 Information and Communication Theory
- 1.1.5 Stochastics and Statistical Physics
- 1.1.6 Intelligent Systems
- 1.1.7 Modeling and Simulation
- 1.1.8 Algorithms and Data Structures
- 1.1.9 Introduction to Control Theory and Optimization
- 1.1.10 Social dynamics
- 1.2 Catch-up Courses
- 1.3 Specialization 1: Communication Networks
- 1.1 Core Courses
- 2 Group Work
Curriculum
Core Courses
The following courses are mandatory. About 60 ECTS.
Introduction to Self-Organizing Networked Systems
- Part I (30h): What is a self-organizing system? Methodology and theory. Giving the big picture. Few mathematics, non-technical. History. Evolution, cybernetics, chaos, emergence, entropy. Links to following courses. Similar to course "complexity and evolution" in Brussels.
- Part II: Case studies. A ring lecture (colloquium) with speakers from different universities and different fields (which can also attended by all university members):
- Self-Organization in Communication and Computer Networks
- Social insects
- Immune system
- Social group dynamics
- Self-Organization in Biology
- Brain dynamics
- Robotics
- Chemical reactions
- Self-organization in linguistics
- Overview of cellular and evolutionary biology
Dynamical Systems
Lecture and Lab
Content: similar to "Nonlinear Dynamics and Chaos" by Steven H. Strogatz
Textbooks:
- Nonlinear Dynamics and Chaos by Steven H. Strogatz
Network Theory
Lecture and Exercises
Content: Networks from the real world. Network topology: Graph theory basics, random graphs, phenomena small wold and scale-freeness. Network functions/processes/algorithms: E.g. search, percolation.
Textbooks:
Information and Communication Theory
Lecture and Exercises
Textbooks:
Stochastics and Statistical Physics
Lecture and Exercises
Content: Selected topics from the following fields: Review of random variables, combination of RVs, Stochastic Processes (Concepts, random walks and other applications, Markov chains, Markov processes and queueing theory). Statistical Physics .
Textbooks:
- Probability, Random Variables, and Stochastic-Processes by Papoulis
- Statistical Physics of Particles by Mehran Kardar
- Fundamentals of Statistical and Thermal Physics by Frederick Reif
Intelligent Systems
Neural networks: introduction to biological neural networks, Artificial Neural Networks, topologies (Multilayer, recurrent, fully meshed), Self-Organizing Feature Maps, spiking neural networks, emergent patterns in ANN
Machine learning: Genetic algorithms, simulated annealing, Sintflut algorithm, rule-based learning, bayesian networks
Modeling and Simulation
Contents:
- Model building, modeling and specification languages (e.g. UML)
- How to do good simulations and data analysis, model validation?
- How to do good empirical studies?
- Data/results representation
- Cellular automata, evolutionary algorithms, multi-agent systems, PDEs
- Group work
Related books:
Algorithms and Data Structures
Lecture and Lab.
Content: Sorting and searching, tree-based structures, graph algorithms (over), recursive algorithms, complexity classes and computational effort.
Textbooks:
- The Algorithm Design Manual by Steven S. Skiena
- Introduction to Algorithms by Charles E. Leiserson, Ronald L. Rivest, Clifford Stein
Introduction to Control Theory and Optimization
control loop, stability, distributed control, event-based control, MIMO control systems
Social dynamics
- Game theory: evolution of cooperation (Prisoner's Dilemma), implications for economic behavior
- Group dynamics: dynamics of consensus and conflict in groups of individuals trying to solve problems together; includes emergent processes such as polarization, groupthink, coordination of language and terminology
- Collective intelligence: conditions under which a group can make better/worse decisions than the individuals it is composed of
Catch-up Courses
Depending on the background of the student, she or he attends a subset of the following courses:
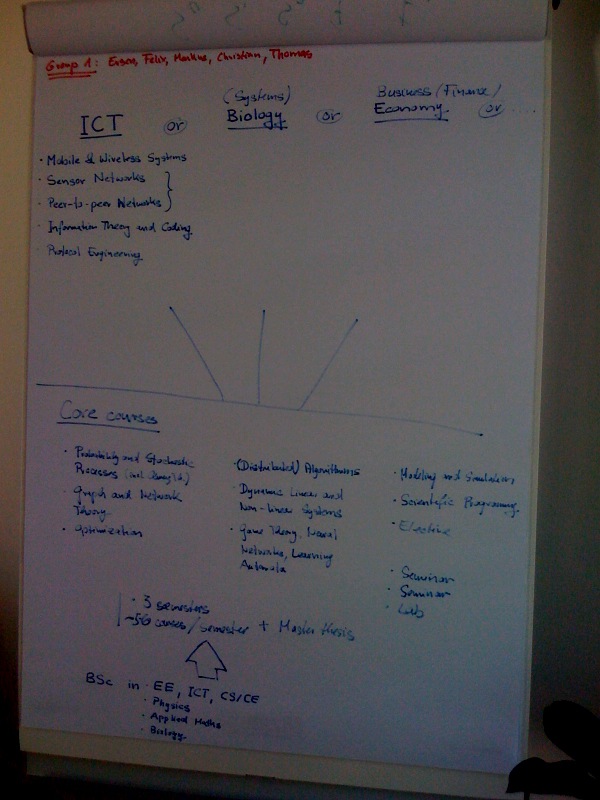
Specialization 1: Communication Networks
Mobile and Wireless Systems
Contents: Introduction and overview. Radio propagation. Coding, modulation, and duplexing. Multiple access and cellular concept. Medium access control (MAC) protocols. Wireless LAN 802.11. Network architecture and mobility protocols. Security in mobile networks. Multihop networks. Economic, health, and social aspects.
Sensor Networks
Peer-to-Peer Networks
Protocol Engineering
Group Work
Curriculum table
| Subject | Type | g1 grad | g2 und.grad | g2 grad | g2 grad spec. | g3 | g4 | |
|---|---|---|---|---|---|---|---|---|
| Dynamical Systems | Lecture | X | X | X | ||||
| Graph and Network Theory | X | X | ||||||
| Optimization | X | |||||||
| Probability and Stochastic | X | |||||||
| Information Theory | Lecture | X | X | |||||
| Algorithms 1 | Lecture & Lab | X | ||||||
| Algorithms 2 | Lecture & Lab | X | ||||||
| Distributed Algorithms | X | X | ||||||
| Game Theory | X | X | ||||||
| Numerical Simulations | Lecture & Labs | X | ||||||
| Modeling and Simulation | Lecture & Labs | X | ||||||
| Topics course SO in nature/society | Lecture | X | X | |||||
| Network 1 | X | X | ||||||
| Network 2 | X | X | ||||||
| Statistical physics 1 & 2 | X | X | ||||||
| Embedded Systems | X | |||||||
| Sensors and Robotics | X | |||||||
| Calculus 1 & 2 | Lecture | X | X | |||||
| Statistics | Lecture | X | ||||||
| Diff. Equations | Lecture | X | X | |||||
| Linear Algebra | Lecture | X | ||||||
| Scientific Programming | Lecture | X | X | |||||
| Natural sciences | Lecture | X | X | |||||
| Mobile&Wireless Systems | X | |||||||
| Sensor Networks | X | |||||||
| Peer-to-Peer Networks | X | |||||||
| Information Theory and Coding | X | X | ||||||
| Protocol Engineering | X | |||||||
| Physics | bacc | |||||||
| Applied Mathematics | bacc | |||||||
| Biology | bacc | X | ||||||
| Economics | X | |||||||
| Business management | X | |||||||
| Conceptual Framework | X | |||||||
| Ethics (Philosophical issues) | X | |||||||
| Bayesian statistics | X | |||||||
| Neural networks | X |
Group 1: Bauschert, Bettstetter, Pletzer, Quaritsch, Yanmaz
Group 2: Anton, Manfred, Felix, Johannes,Alain
All courses should specifically deal with applications towards SOS.
Group 3: Francis, Marc, Mariam, Nikolaj, Raissa,
For Master program the requirements are basics of differential equations, calculus, PDEs.
Comments to some courses:
Computational techniques: agent-based models, genetic algorithms, cellular automata.
Statistical Physics: phase transition, entropy, combinatorics/ensembles.
Biology: focus on cellular and evolutionary biology.
Distributed control and communications.
Tools (computational): CellSim, R, virtual laboratory, as well as for visualizing dynamical systems, basins of attraction.
Mathematical tools: MAtheatica, Matlab.
Group work methods, project-based learning, Wiki.